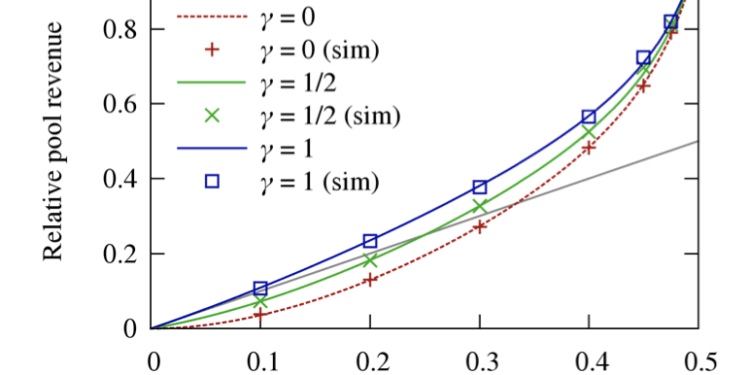
The 2013 selfish-mining paper by Ittay Eyal and Emin Gün Sirer [0] introduces a variable γ:
We denote by γ the ratio of sincere miners that select to mine on the pool’s block, and the opposite (1−γ) of the non-pool miners mine on the opposite department.
The essential thought is that the attacker pool withholds their block till they study a competing block from an sincere miner. Since sincere nodes favor the primary block they see, this variable expresses the power of the attacker to race their block in entrance of the sincere block.
Particularly this refers back to the fraction of miner nodes that see the attacking block first. As defined of their simulation part:
We assume block propagation time is negligible in comparison with mining time, as is the case in actuality. Within the case of two branches of the identical size, we artificially divide the non-pool miners such {that a} ratio of γ of them mine on the pool’s department and the remaining mine on the opposite department.
The simulation produces determine 2:
I am confused about probably the most pessimistic state of affairs γ=0, i.e. any time the attacker pool tries to race in entrance of the sincere block they fail miserably. Intuitively I might count on such a pool to constantly lose cash, so why does not the crimson line keep under the gray line?
Is there some further assumption within the paper that I am lacking?